The self-consistency (CT) inference strategy was introduced in the paper “Self-Consistency Improves Chain of Thought Reasoning in Language Models”, published in March 2022. In essence, the CT approach is simply to perform multiple inferences, and use the most frequent answer.

In the CT approach, we first prompt the language model with chain-of-thought (CoT) prompting. Then instead of greedily decoding the optimal reasoning path, first sample from the language model’s decoder to generate a diverse set of reasoning paths. Then determine which is the most consistent answer in the final answer set. The following Figure (from the paper) illustrates the approach:

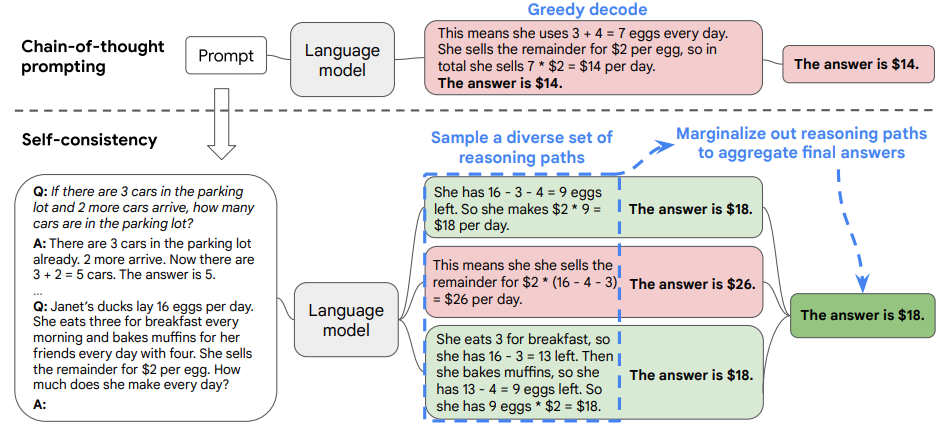
Such an approach is analogous to the human experience that if multiple different ways of thinking lead to the same answer, one has greater confidence that the final answer is correct. Self-consistency acts more like a “self-ensemble” that works on top of a single language model.

The authors showed that CT improves over a variety of models. And it complements chain-of-thought prompting.

Selection Model:

• Given a prompt and question, we sample pairs of (rationale, answer) from the decoder. Using the 3rd reasoning path in the Figure above (bottom light green box) as an example.
  • Denote reasoning path $\mathbb{r_i}$ = “She eats 3 for breakfast, so she has 16 - 3 = 13 left. Then she bakes muffins, so she has 13 - 4 = 9 eggs left. So she has 9 eggs * $2 = $18.”
  • Denote final answer $\mathbb{a_i}$ = “The answer is $18”
• Assume we sampled pairs of $(r_i, a_i)$, where $i = 1, \ldots, m$ from the decoder. Then for each unique answer $a$, we calculate: \(P(a|\text{prompt}, \text{question}) = \sum_{i=1}^{m} \mathbf{1}(a_i = a) P(r_i, a_i | \text{prompt}, \text{question})\) \(P(r_i, a_i | \text{prompt, question}) = \text{exp}^{\frac{1}{K} \sum_{k=1}^{K} \text{log }P(t_k | \text{prompt, question}, t_1, \ldots, t_{k-1})}\)
  • Where $K$ is the number of tokens in $(r_i, a_i)$
  • In the end, the authors found that taking a majority vote directly over $a_i$, i.e. $\sum_{i=1}^{m} \mathbb{1} (a_i = a)$ gives very similar performance as compared to taking its weighted sum.

Evaluation

• Dataset and tasks: arithmetic reasoning, commonsense reasoning, symbolic reasoning.
• Language models: evaluated self-consistency overy UL2 (encoder-decoder that is based on T5), GPT-3 175B, LaMDA-137B, PaLM-540B.
• Results are averaged over 10 runs. In each run, sampled 40 outputs from the decoder.