The rotary position embedding method was introduced in the paper “RoFormer: Enhanced Transformer with Rotary Position Embedding” in April-2021.

Introduction

Let us first define some notations:

• $x_i \in \mathbb{R}^{d}$: the d-dimensional word embedding vector for token $w_i$, without position information.
• $q_m = f_{q}(x_m, m)$:
  • $q_m$: query representation of token at position $m$.
  • $f_{q}(x_m, m)$ incorporates the $x_m$ embedding vector and position $m$.
• $k_n = f_{k}(x_n, n)$, $v_n = f_{v}(x_n, n)$: key and value representation of the token at position $n$.
• $a_{m,n} = \frac{\text{exp}(\frac{q_{m}^{T} k_{n}}{\sqrt{d}})}{\sum\limits_{j=1}^{N} \text{exp}(\frac{q_{m}^{T} k_{j}}{\sqrt{d}})}$: attention score between tokens at position $m$ and $n$.
• $o_{m} = \sum\limits_{n=1}^{N} a_{m,n} v_{n}$: output is a weighted sum over the value representations.

A typical choice for the function $f$ is the absolute position embedding, where position information is additive to the semantic word embedding vector: \(f_{t: t \in \{q,k,v\}}(x_i, i) = \mathbf{W}_{t: t \in \{q,k,v\}}(x_i + p_i)\) where the position embedding $p_i \in \mathbb{R}^{d}$ depends on the position of token $w_i$.

Rotary Position Embedding

Given a token at position $m$ which is represented by an embedding vector $x_m$, the main idea to infuse it with position information, is to perform a linear (rotation) transformation on $x_m$ , where the degree of rotation depends on position $m$.

To illustrate, let us assume that $x_m$ is a 2-d vector $[x_{m}^{(1)}, x_{m}^{(2)}]$. Let $\mathbf{W}_{{q,k}}$ denote the $d \times d$ (in this case $2 \times 2$) learnable matrix $\mathbf{W}$.

As the following Figure from https://mathworld.wolfram.com/RotationMatrix.html show, to rotate the vector $v_0$ by a degree $\theta$, we can use the rotation matrix: \(\begin{bmatrix} \text{cos}\theta & \text{-sin}\theta \\ \text{sin}\theta & \text{cos} \theta \end{bmatrix}\)

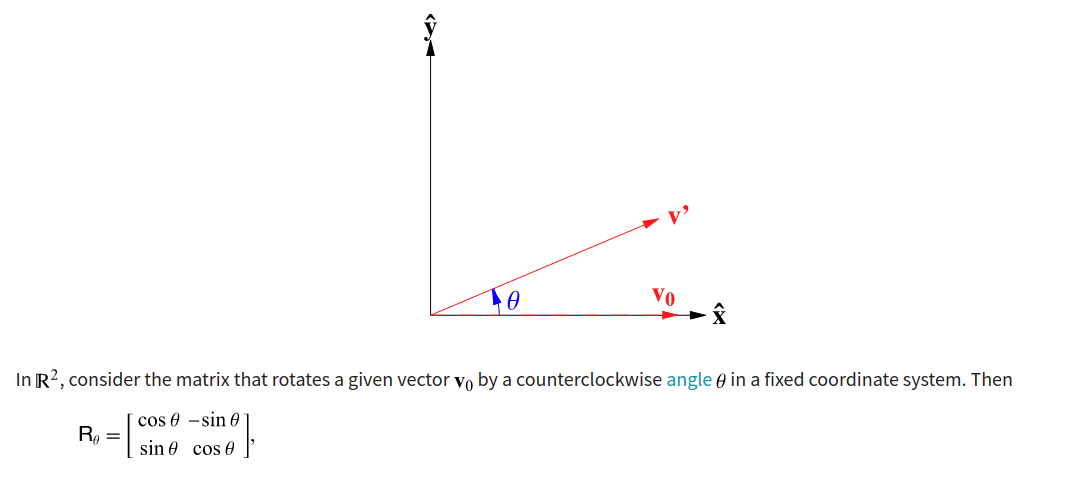
To take position $m$ into account, we scale the degree $\theta$ by $m$, giving rise to the following fuction $f$ which takes the embedding vector $x_m$ and position $m$ into account: \(f_{\{q,k\}}(x_m, m) = \begin{bmatrix} \text{cos }m\theta & \text{-sin }m\theta \\ \text{sin }m\theta & \text{cos }m\theta \end{bmatrix} \begin{bmatrix} W_{\{q,k\}}^{(11)} & W_{\{q,k\}}^{(12)} \\ W_{\{q,k\}}^{(21)} & W_{\{q,k\}}^{(22)} \end{bmatrix} \begin{bmatrix} x_{m}^{(1)} \\ x_{m}^{(2)}\end{bmatrix}\)

In the above, we assume that the embedding vector $x_{m}$ is just 2 dimension in length, and the matrix $W$ is the usual query $q$ or key $k$ in self-attention.

Generalization to $d$ dimension

To generalize the above result from $x_i$ in 2-d to $\mathbb{R}^{d}$, we define the rotation matrix as follows: \(\mathbf{R}_{\Theta,m}^{d} = \begin{bmatrix} \text{cos }m\theta_{1} & -\text{sin }m\theta_{1} & 0 & 0 & \ldots & 0 & 0 \\ \text{sin }m\theta_{1} & \text{cos }m\theta_{1} & 0 & 0 & \ldots & 0 & 0 \\ 0 & 0 & \text{cos }m\theta_{2} & -\text{sin }m\theta_{2} & \ldots & 0 & 0 \\ 0 & 0 & \text{sin }m\theta_{2} & \text{cos }m\theta_{2} & \ldots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \cdots & \text{cos }m\theta_{d/2} & -\text{sin }m\theta_{d/2} \\ 0 & 0 & 0 & 0 & \cdots & \text{sin }m\theta_{d/2} & \text{cos }m\theta_{d/2} \end{bmatrix}\)

Computational efficiency

Instead of taking $\mathbf{R}_{\Theta,m}^{d}$ and performing a $d \times d$ matrix multiplication, we note that the roation matrix is sparse, which allows us to do a more computational efficient calculation:

\[\mathbf{R}_{\Theta,m}^{d}x = \begin{bmatrix} x_1\\x_2\\x_3\\x_4\\ \vdots \\x_{d-1}\\x_{d} \end{bmatrix} \otimes \begin{bmatrix} \text{cos }m\theta_{1} \\ \text{cos }m\theta_{1} \\ \text{cos }m\theta_{2} \\ \text{cos }m\theta_{2} \\ \vdots \\ \text{cos }m\theta_{d/2} \\ \text{cos }m\theta_{d/2} \end{bmatrix} + \begin{bmatrix} -x_2\\x_1\\-x_4\\x_3\\ \vdots \\-x_{d}\\x_{d-1} \end{bmatrix} \otimes \begin{bmatrix} \text{sin }m\theta_{1} \\ \text{sin }m\theta_{1} \\ \text{sin }m\theta_{2} \\ \text{sin }m\theta_{2} \\ \vdots \\ \text{sin }m\theta_{d/2} \\ \text{sin }m\theta_{d/2} \end{bmatrix}\]