We define two common information retrieval (IR) metrics: MAP@K and NDCG.

MAP@K

Mean Average Precision at K (MAP@K): are the predicted items relevant? Are the most relevant items on top?

• MAP of a set of queries = $\frac{\sum_{q=1}^{Q}AP(q)}{Q}$
• $\text{P@K} = \frac{\text{number of relevant items in top K results}}{K}$
• $\text{AP@K} = \frac{1}{\text{GTP}} \sum_{k=1}^{N} \text{P@K} \times \text{rel}@K$
  • GTP: total number of ground truth positives
  • rel@K: indicator function which equals 1 if document at rank $k$ is relevant, 0 otherwise

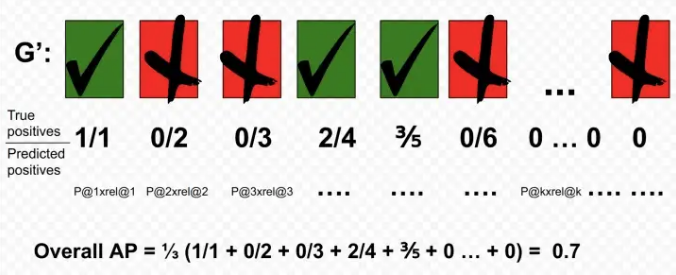
• If all the relevant documents are returned at the front, then AP is a perfect 1.0. Hence, $AP$ metric penalize models that are not able to return a ranked list with true positives leading the list.

NDCG

Normalized Discounted Cumulative Gain

• Cumulative Gain (CG) = $\sum_{i=1}^{n}r_i$
  • for a recommendation set of $n$ documents, $r_i$ is relevance of document $i$
  • to inject position aware scoring, we do DCG
• Discounted CG (DCG) = $\sum_{i=1}^{n} \frac{r_i}{log_{2}(i+1)}$
  • An alternative expression is $\sum_{i=1}^{n} \frac{2^{r_i}-1}{log_{2}(i+1)}$, which penalizes more heavily (vs the above expression), if documents with higher relevance are ranked lower.
  • If relevance scores are binary (0 or 1), then the 2 expressions are equal
  • Example. Let’s look at 2 rankings. Set-A = [2,3,3,1,2], Set-B = [3,3,2,2,1]
    • $DCG_{A} = \frac{2}{log_{2}(1+1)} + \frac{3}{log_{2}(2+1)} + \frac{3}{log_{2}(3+1)} + \frac{1}{log_{2}(4+1)} + \frac{2}{log_{2}(5+1)} \approx 6.64$
    • $DCG_{B} = \frac{3}{log_{2}(1+1)} + \frac{3}{log_{2}(2+1)} + \frac{2}{log_{2}(3+1)} + \frac{2}{log_{2}(4+1)} + \frac{1}{log_{2}(5+1)} \approx 7.14$
  • Con of DCG: it is an absolute score. The more relevant documents that a query has, the higher the DCG score. But each query will have different number of relevant documents. Hence we do NDCG, which bounds the score to 0.0 - 1.0.
• Normalized DCG (NDCG) = $\frac{DCG}{iDCG}$
  • Compute DCG of recommended/predicted order. Compute DCG of ideal order (iDCG).
  • For the above examples, NDCG = $\frac{6.64}{7.14} \approx 0.93$