Gradient check-pointing is one of the techniques we can use to reduce the memory footprint when training transformer models. To compute the forward pass and backward pass for a compute graph, a usual strategy is to use and compute values “as soon as possible”. For instance, in the following figure which represents a computation graph, the forward pass (top row) activations are computed (once) and then stored in memory. This allows input to the backward pass (bottom row) computations. However, storing all activations is memory intensive.

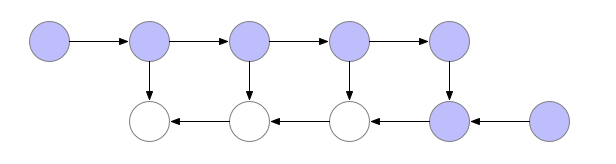
Another strategy that uses the minimal amount of memory, is computing values “as late as possible”. This means that we compute activation value at time step $t$, but discard it from memory as soon as it has been used to compute the activation value for the next time step $t+1$. Illustrating with the same computation graph:

• We see in the following figure that the last activation has been computed. This is the top row rightmost blue node, and let us denote this with $a_{l}$. Note that since we are using the strategy of using minimal memory, all earlier activations $a_0 \ldots a_{l-1}$ had been computed but discarded.
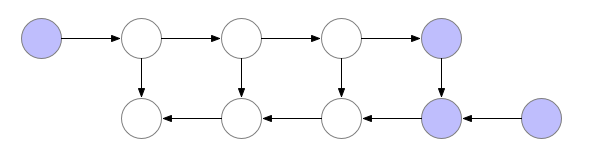
  • Comparing $a_{l}$ against the target value (bottom row rightmost blue node) allows us to compute the first backward pass value (bottom row blue node which accepts 2 incoming edges; let us denote this with $b_{l}$).
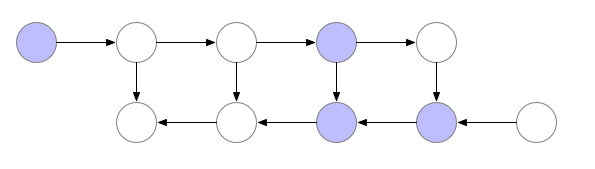
• However, to compute the next backward pass value $b_{l-1}$, we also require input from the 2nd last activation node $a_{l-1}$, which we had earlier computed but discarded. Thus, we need to perform another forward pass to recalculate $a_{l-1}$, before we can feed it together with $b_{l}$, in order to calculate $b_{l-1}$, as shown in the following figure.

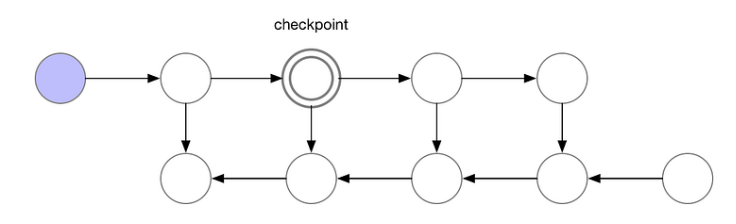
A middle ground between minimizing memory usage vs performing recomputations, is to save some of the intermediate results so that we do not need to recompute them again. These saved results/nodes are called checkpoints, e.g. we could use the following circled node as a checkpoint:

• For a computation chain of length $n$, a general strategy is to place checkpoints every $\sqrt{n}$ steps. The following summarizes the memory and computation requirements of the above 3 strategies:

  Strategy	memory requirement	computation requirement
  “as soon as possible”	O(n)	O(n)
  “as late as possible”	O(1)	O($n^2$)
  check-pointing	O($\sqrt{n}$)	O(n)